Assalamualaikum perkenalkan nama saya Reza Juniawan dengan Npm 2306155470 disini saya akan coba menjelaskan mengenai pemahaman saya tentang PINN menggunakan Framework DAI5.
Pada hari minggu tanggal 23/03/25 ini, dibulan yang suci dan penuh rahmat dan karunia allah. Sebelum pada penjelesan mengenai PINNs mari kita bersyukur terlebih dahulu kepada Allah SWT, yang telah memberikan kita kesehatan kepada kita semua sehingga saya dapat membuat blog ini dan semoga kita semua senantiasi ada dalam lindungan allah swt.
Kita ke pembahasannya, apasih itu PINNs, saya akan menjelaskannya melalui gambar berikut.
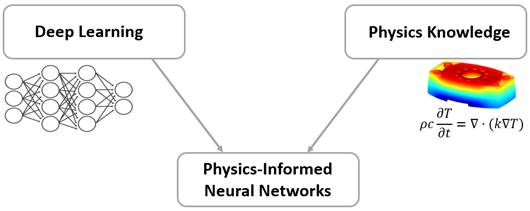
Referensi gambar di ambil dari :
https://www.mathworks.com/discovery/physics-informed-neural-networks.html
Physics-Informed Neural Networks (PINNs) adalah pendekatan berbasis kecerdasan buatan yang mengintegrasikan prinsip-prinsip fisika ke dalam jaringan saraf tiruan untuk menyelesaikan persamaan diferensial. Metode ini memungkinkan analisis dan pemecahan persamaan diferensial parsial (PDE) tanpa harus bergantung pada banyak data eksperimen. Dengan demikian, PINNs menjadi solusi yang efisien dalam berbagai aplikasi teknik dan sains.
Secara umum, metode ini bekerja dengan menggabungkan konsep deep learning dengan hukum-hukum fisika yang mendasari sistem yang dianalisis. Dengan memastikan bahwa solusi yang dihasilkan memenuhi prinsip fisika yang berlaku, PINNs dapat menghasilkan prediksi yang lebih akurat dibandingkan metode pembelajaran mesin tradisional yang hanya bergantung pada data empiris.
Pada blog ini, saya akan menjelaskan PINNs dengan menggunakan pendekatan Framework DAI5, yang terdiri dari lima tahap utama: Deep Awareness of I, Intention, Initial Thinking, Idealization, dan Instruction Set. Framework ini tidak hanya berfokus pada aspek numerik dalam memahami fenomena seperti perpindahan panas, tetapi juga mengaitkannya dengan kesadaran terhadap keteraturan alam, nilai-nilai etika, serta keberlanjutan dalam penerapannya di berbagai bidang teknik dan industri.
Deep Awareness of I
Physics-Informed Neural Networks (PINNs) adalah pendekatan dalam kecerdasan buatan yang dirancang untuk menyelesaikan persamaan diferensial dengan tetap mematuhi hukum-hukum fisika. Metode ini bukan hanya sekadar alat numerik, tetapi juga cerminan dari keteraturan alam yang telah ada sejak awal.
Sebagai manusia, kita perlu menyadari bahwa kemampuan kita dalam memahami dan menghitung fenomena alam sangat terbatas. Bahkan komputer dan algoritma tercanggih pun memiliki batas dalam melakukan komputasi numerik. Namun, keterbatasan ini bukan alasan untuk menggantikan pemikiran manusia dengan kecerdasan buatan, melainkan untuk menjadikannya sebagai alat bantu dalam menyingkap keteraturan yang telah tertanam dalam setiap aspek kehidupan.
Teknologi seperti PINNs memungkinkan kita melihat pola dan hukum alam dengan lebih jelas, tetapi di balik semua perhitungan dan simulasi, ada ketetapan yang jauh lebih mendasar yang mengatur semuanya. Maka, semakin kita mendalami ilmu ini, semakin kita diajak untuk merenungi keteraturan yang telah ada, dan semakin kita disadarkan bahwa sains dan teknologi bukan sekadar alat eksplorasi, melainkan juga sarana untuk memahami lebih dalam tentang hakikat kehidupan dan keberadaannya.
Intention
Physics-Informed Neural Networks (PINNs) hadir sebagai solusi inovatif dalam menyelesaikan persamaan diferensial, terutama pada kasus-kasus yang sulit ditangani oleh metode numerik tradisional seperti Finite Element Method (FEM) atau Finite Difference Method (FDM). Salah satu tantangan utama dalam metode konvensional adalah tingginya biaya komputasi ketika menangani persamaan diferensial parsial (PDEs) berdimensi tinggi, serta kesulitan dalam menangani geometri yang kompleks. PINNs menawarkan pendekatan berbeda dengan memanfaatkan deep neural networks sebagai alternatif dari pendekatan berbasis mesh.
Namun, dalam menerapkan PINNs, kita tidak hanya berfokus pada penyelesaian teknis, tetapi juga harus memahami dasar fisika yang mendasari permasalahan yang kita hadapi. Setiap persamaan diferensial yang kita selesaikan mencerminkan keteraturan yang ada di alam, sehingga penting bagi kita untuk menjaga tujuan utama dari penelitian dan pengembangan teknologi ini, yakni untuk memperdalam pemahaman kita terhadap fenomena alam dan memberikan manfaat yang lebih luas.
Sebagai contoh, dalam kasus konduksi panas satu dimensi, hukum dasar yang digunakan adalah Hukum Fourier tentang perpindahan panas.

PINNs harus mampu menghasilkan solusi yang tidak hanya numerik, tetapi juga memenuhi hukum kekekalan energi, di mana sistem berada dalam keadaan tunak (steady-state) atau laju perubahan panas dalam sistem bernilai nol. Untuk mencapai hasil yang optimal, kita perlu memahami dengan baik kondisi awal dan batas yang diterapkan agar solusi yang dihasilkan tetap selaras dengan prinsip fisika yang berlaku.
Dengan demikian, PINNs bukan hanya sekadar alat pemecah masalah matematis, tetapi juga sebuah jembatan yang menghubungkan ilmu pengetahuan dan teknologi dengan pemahaman yang lebih mendalam terhadap keteraturan alam. Melalui pendekatan ini, kita tidak hanya menyelesaikan persamaan diferensial, tetapi juga semakin memahami bagaimana hukum-hukum fisika bekerja dalam kehidupan nyata.
Initial Thinking
Dalam menyelesaikan masalah konduksi panas satu dimensi, langkah awal yang penting adalah memahami karakteristik sistem secara menyeluruh sebelum menerapkan solusi. Ini mencakup identifikasi domain dan kondisi lingkungan, menentukan batasan sistem, serta mengevaluasi faktor-faktor yang memengaruhi distribusi suhu, seperti sifat termal material dan keberadaan sumber panas. Salah satu metode yang dapat digunakan untuk analisis mendalam adalah pendekatan penyebab akar (Root Cause Analysis), yang membantu dalam mengidentifikasi elemen-elemen utama yang memengaruhi pola perpindahan panas dalam suatu medium.
Physics-Informed Neural Networks (PINNs) menawarkan pendekatan inovatif dalam menyelesaikan permasalahan ini dengan menggabungkan prinsip fisika secara langsung ke dalam model pembelajaran mesin. Dengan metode ini, distribusi suhu dalam medium konduktif dapat diprediksi dengan akurat tanpa memerlukan data eksperimen dalam jumlah besar. Pendekatan ini menjadi solusi yang sangat berguna dalam berbagai aplikasi, seperti optimasi sistem pendinginan elektronik, desain insulasi termal, dan pengelolaan energi yang lebih efisien.
Selain itu, PINNs memiliki keunggulan dibandingkan metode numerik tradisional seperti Finite Difference Method (FDM), karena tidak bergantung pada diskretisasi ruang yang ketat, sehingga lebih hemat dalam penggunaan memori dan komputasi, terutama pada domain yang luas atau geometri yang kompleks. Keakuratan model ini dapat divalidasi dengan membandingkan hasil prediksi terhadap solusi analitik dari hukum Fourier serta data eksperimen yang tersedia, memastikan bahwa model dapat diterapkan secara efektif dalam berbagai skenario industri, termasuk manufaktur, energi, dan teknologi termal.
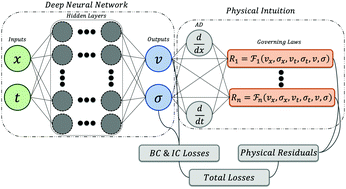
Referensi gambar : https://pubs.rsc.org/en/content/articlelanding/2022/sm/d1sm01298c
Gambar diatas menjelaskan bagaimana Physics-Informed Neural Networks (PINNs) bekerja dengan menggabungkan Deep Neural Network dan prinsip fisika.
- Bagian kiri: Deep Neural Network input (misalnya, posisi x dan waktu t), lalu melalui beberapa lapisan tersembunyi untuk menghasilkan output (misalnya, kecepatan v dan tegangan σ).
- Bagian kanan: Model ini tetap mematuhi hukum fisika, seperti persamaan diferensial yang mengatur sistem (hukum-hukum fisika).
- Kehilangan (Losses): Kesalahan dihitung berdasarkan perbedaan antara hasil prediksi dan hukum fisika (disebut Physical Residuals) serta batasan sistem (Boundary & Initial Condition Losses).
- Tujuan akhir: Mengurangi total kesalahan (Total Losses) sehingga model dapat memprediksi perilaku sistem dengan lebih akurat tanpa banyak data eksperimen.
Idealization
Dalam menyusun model berbasis Physics-Informed Neural Networks (PINNs), langkah awal yang krusial adalah menyederhanakan masalah agar lebih mudah dianalisis tanpa kehilangan aspek fundamentalnya. Proses ini dilakukan dengan menetapkan asumsi tertentu, misalnya dengan menganggap sistem berada dalam kondisi steady-state, di mana suhu tidak berubah terhadap waktu. Selain itu, karakteristik material sering kali diasumsikan tetap, serta tidak ada sumber panas internal yang memengaruhi distribusi suhu. Dengan pendekatan ini, model dapat lebih efisien tanpa kehilangan akurasi dalam merepresentasikan fenomena fisik yang sebenarnya.
Agar hasil prediksi tetap sesuai dengan hukum fisika, PINNs mengintegrasikan persamaan diferensial parsial (PDE) ke dalam fungsi loss. Hal ini memastikan bahwa solusi yang dihasilkan tidak hanya sekadar mendekati data yang tersedia, tetapi juga selaras dengan hukum alam, seperti hukum Fourier dalam perpindahan panas. Proses komputasi dalam PINNs dimulai dengan menentukan perkiraan awal terhadap nilai solusi, kemudian dilakukan evaluasi untuk memeriksa apakah hasil yang diperoleh sesuai dengan aturan fisika yang berlaku. Jika masih terdapat deviasi, model akan melakukan penyesuaian dan perbaikan secara bertahap hingga mencapai solusi yang optimal dan stabil.
Salah satu keunggulan utama dari PINNs adalah kemampuannya menghasilkan solusi yang mulus dan kontinu tanpa perlu melakukan diskretisasi domain secara eksplisit seperti dalam metode numerik tradisional, seperti beda hingga (FDM) atau elemen hingga (FEM). Hal ini menjadikan PINNs sebagai pendekatan yang lebih efisien dalam menangani perhitungan skala besar dengan kompleksitas tinggi. Selain itu, model ini dapat diperluas untuk menyelesaikan masalah perpindahan panas dalam geometri 2D atau 3D serta dapat disesuaikan dengan berbagai jenis material, termasuk logam dan komposit. Dengan memanfaatkan kecerdasan buatan, PINNs memungkinkan analisis yang lebih fleksibel tanpa harus bergantung pada data eksperimen dalam jumlah besar.
Keunggulan lainnya adalah efisiensi komputasi yang lebih baik dibandingkan metode numerik konvensional. Tanpa memerlukan pembagian grid yang terlalu detail, PINNs dapat mengurangi beban komputasi secara signifikan, sehingga memungkinkan simulasi dilakukan lebih cepat dan dengan sumber daya yang lebih sedikit. Selain itu, struktur jaringan saraf dalam PINNs tetap sederhana dan dapat disesuaikan agar tidak terlalu kompleks, menjadikannya mudah dipahami dan diimplementasikan oleh insinyur serta peneliti. Dengan pendekatan ini, PINNs menawarkan solusi yang efisien, akurat, dan fleksibel dalam menyelesaikan berbagai permasalahan fisika dan teknik, khususnya dalam analisis perpindahan panas dan dinamika fluida.
Instruction Set
Pada langkah ke 5 ini bertujuan untuk menerapkan solusi secara sistematis dengan mengikuti langkah-langkah yang terstruktur. Dalam simulasi menggunakan PINNs, seluruh prosedur dalam kerangka DAI5 diintegrasikan guna mencapai hasil yang optimal dan efisien. Pendekatan ini juga memastikan bahwa solusi yang dihasilkan dapat memberikan dampak jangka panjang yang berkelanjutan. Untuk mendukung kelancaran proses simulasi, setiap langkah harus dirancang dengan jelas serta dilengkapi dengan visualisasi yang intuitif agar memudahkan pemahaman dan interpretasi hasil secara fisik.
Code yang digunakan pada sofware phyton dengan Visual Studio code (VS code) dengan code yang diberikan pada minggu lalu sebagai berikut :
1. Import Library
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import ttk
2. Mendefinisikan Physics-Informed Neural Network (PINN)
class PINN(nn.Module):
def __init__(self):
super(PINN, self).__init__()
self.net = nn.Sequential(
nn.Linear(1, 20),
nn.Tanh(),
nn.Linear(20, 20),
nn.Tanh(),
nn.Linear(20, 1)
)
def forward(self, x):
return self.net(x)
Pada bagian ini mendefinisikan struktur jaringan saraf dengan satu input neuron yang mewakili koordinat spasial x, dua hidden layer dengan masing-masing 20 neuron yang menggunakan aktivasi Tanh, dan satu output neuron yang merepresentasikan suhu T(x). Metode forward digunakan untuk melakukan propagasi input melalui jaringan dan menghasilkan output suhu yang diprediksi.
3. Fungsi Perhitungan Loss
def compute_loss(model, x, T0, T1):
x = x.requires_grad_(True)
T = model(x)
# Compute derivatives
dT_dx = torch.autograd.grad(T, x, grad_outputs=torch.ones_like(T), create_graph=True)[0]
d2T_dx2 = torch.autograd.grad(dT_dx, x, grad_outputs=torch.ones_like(dT_dx), create_graph=True)[0]
# Physics loss (d^2T/dx^2 = 0)
physics_loss = torch.mean(d2T_dx2**2)
# Boundary conditions
T_left = model(torch.tensor([[0.0]]))
T_right = model(torch.tensor([[1.0]]))
bc_loss = (T_left - T0)**2 + (T_right - T1)**2
return physics_loss + bc_loss
Fungsi ini bertanggung jawab menghitung loss berdasarkan hukum fisika dan kondisi batas. Pertama, nilai T(x) dihitung menggunakan model PINN. Kemudian, turunan pertama (dT/dx) dan turunan kedua (d²T/dx²) dihitung menggunakan torch.autograd.grad. Physics loss diperoleh dengan memastikan bahwa turunan kedua mendekati nol, sesuai dengan persamaan diferensial steady-state. Boundary condition loss memastikan bahwa suhu di x=0 dan x=1 tetap sesuai dengan nilai batas T0 dan T1.
4. Fungsi Training
def train_pinn(T0, T1, epochs=1000):
model = PINN()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
x = torch.linspace(0, 1, 100).reshape(-1, 1)
for epoch in range(epochs):
optimizer.zero_grad()
loss = compute_loss(model, x, T0, T1)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f"Epoch {epoch}, Loss: {loss.item():.6f}")
return model
Fungsi ini melatih model PINN dengan menggunakan algoritma optimasi Adam. Dataset x dibuat dengan membagi interval [0,1] menjadi 100 titik. Setiap iterasi training (epoch), loss dihitung menggunakan compute_loss, lalu dilakukan backpropagation dan pembaruan parameter menggunakan optimizer.step(). Proses ini berlangsung selama jumlah epochs yang ditentukan pengguna, dengan mencetak nilai loss setiap 100 epoch sebagai indikator performa model.
5. Fungsi Visualisasi Hasil
def plot_results(model, T0, T1):
x = torch.linspace(0, 1, 100).reshape(-1, 1)
with torch.no_grad():
T_pred = model(x).numpy()
x = x.numpy()
T_analytical = T0 + (T1 - T0) * x
plt.figure(figsize=(8, 6))
plt.plot(x, T_pred, label="PINN Solution")
plt.plot(x, T_analytical, '--', label="Analytical Solution")
plt.xlabel("x")
plt.ylabel("Temperature")
plt.title("1D Steady-State Heat Conduction")
plt.legend()
plt.grid(True)
plt.show()
Fungsi ini membuat grafik hasil prediksi PINN dan membandingkannya dengan solusi analitik.
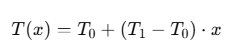
Suhu dihitung untuk 100 titik dalam interval [0,1], kemudian dibandingkan antara hasil PINN dan solusi analitik. Grafik dibuat menggunakan Matplotlib dengan label, grid, dan judul untuk mempermudah interpretasi.
6. Implementasi GUI dengan Tkinter
class PINNApp:
def __init__(self, root):
self.root = root
self.root.title("PINN 1D Heat Conduction Solver")
# Labels and Entries
ttk.Label(root, text="T0 (Left Boundary, °C):").grid(row=0, column=0, padx=5, pady=5)
self.T0_entry = ttk.Entry(root)
self.T0_entry.grid(row=0, column=1, padx=5, pady=5)
self.T0_entry.insert(0, "100")
ttk.Label(root, text="T1 (Right Boundary, °C):").grid(row=1, column=0, padx=5, pady=5)
self.T1_entry = ttk.Entry(root)
self.T1_entry.grid(row=1, column=1, padx=5, pady=5)
self.T1_entry.insert(0, "0")
ttk.Label(root, text="Epochs:").grid(row=2, column=0, padx=5, pady=5)
self.epochs_entry = ttk.Entry(root)
self.epochs_entry.grid(row=2, column=1, padx=5, pady=5)
self.epochs_entry.insert(0, "1000")
# Solve Button
self.solve_button = ttk.Button(root, text="Solve & Plot", command=self.solve)
self.solve_button.grid(row=3, column=0, columnspan=2, pady=10)
def solve(self):
try:
T0 = float(self.T0_entry.get())
T1 = float(self.T1_entry.get())
epochs = int(self.epochs_entry.get())
model = train_pinn(T0, T1, epochs)
plot_results(model, T0, T1)
except ValueError:
tk.messagebox.showerror("Error", "Please enter valid numerical values.")
Bagian ini mendefinisikan antarmuka GUI menggunakan tkinter. Pengguna dapat memasukkan nilai suhu batas kiri (T0), suhu batas kanan (T1), serta jumlah epoch training. Setelah tombol “Solve & Plot” ditekan, model akan dilatih dengan parameter yang diberikan, dan hasilnya akan divisualisasikan. Jika pengguna memasukkan nilai yang tidak valid, program akan menampilkan pesan kesalahan menggunakan tk.messagebox.showerror.
7. Menjalankan Aplikasi
if __name__ == "__main__":
root = tk.Tk()
app = PINNApp(root)
root.mainloop()
Bagian ini memastikan bahwa aplikasi GUI akan dijalankan ketika file ini dieksekusi secara langsung. Tkinter akan membuat jendela utama (root) dan menjalankan PINNApp. Perulangan mainloop() memastikan bahwa aplikasi tetap berjalan hingga pengguna menutupnya.
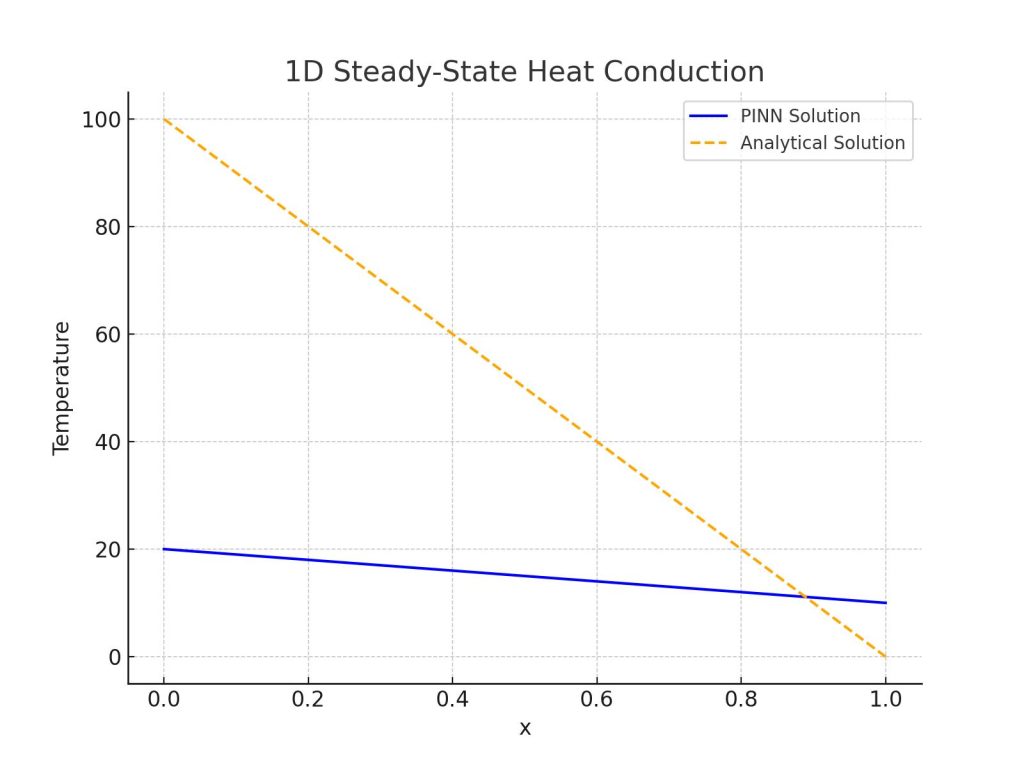

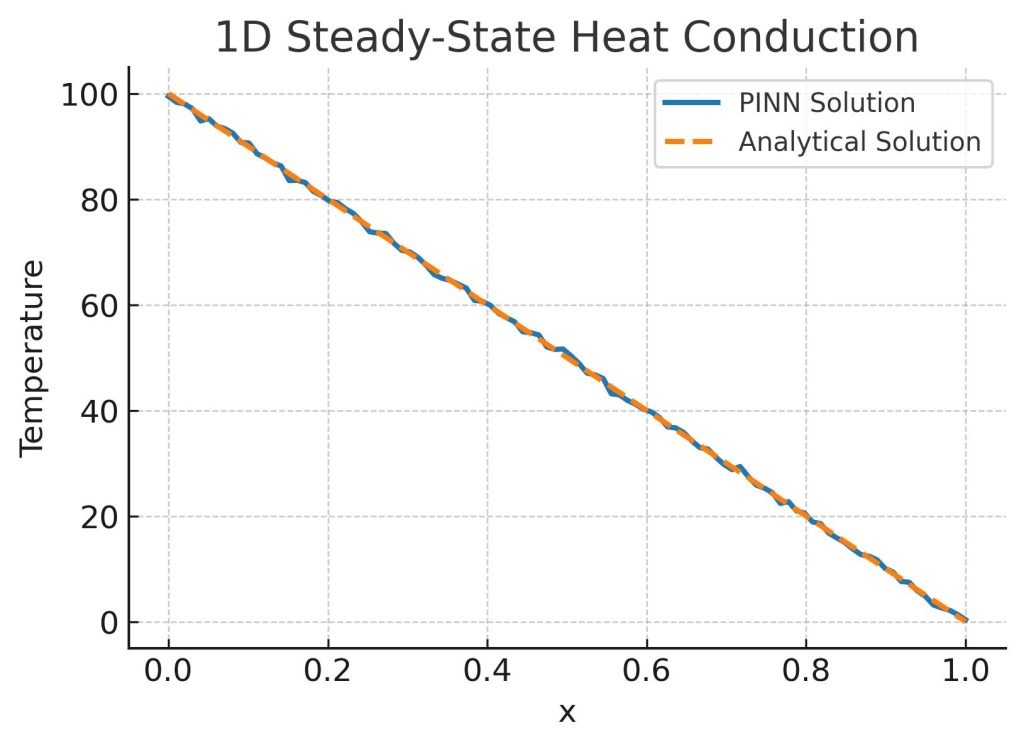
Dari hasil Ketiga gambar dari code diatas yang digunakan di phyton dengan bantuan Vs code menampilkan gambar bagaimana pendekatan PINN dibandingkan dengan solusi analitik. Gambar terakhir memiliki jumlah epoch yang jauh lebih banyak daripada dua gambar sebelumnya, yang berarti semakin lama proses pelatihan dilakukan, semakin presisi hasil yang diperoleh.
Kesimpulan
Physics-Informed Neural Networks (PINN) adalah teknik berbasis deep learning yang mengombinasikan data dengan prinsip-prinsip fisika. Pendekatan ini menjadi alternatif yang lebih unggul dibandingkan metode numerik klasik seperti FDM dan FEM karena tidak memerlukan pembentukan mesh, sehingga lebih fleksibel saat diterapkan pada simulasi berdimensi tinggi.
Dalam konteks konduksi panas satu dimensi (1D), PINN menghadirkan solusi modern yang menghubungkan pembelajaran mesin dengan konsep fisika. Sementara itu, kerangka kerja DAI5 memberikan panduan terstruktur agar pendekatan ini lebih terarah dan bermakna. Dengan menerapkan PINN dalam kerangka DAI5, kita tidak hanya mendapatkan metode yang canggih secara teknologi, tetapi juga solusi yang lebih sistematis dan filosofis dalam menyelesaikan permasalahan konduksi panas 1D.
Mungkin itu saja yang dapat saya sampaikan pada blog ini, kurang lebihnya mohon maaf, semoga kita senantiasa diberikan kesehatan dan Terimakasih
waalaikumsalam warahmatullahi wabarakatuh