ccitonline.com

A. Project Title

AI Assistant Komputasi Teknik Untuk Perhitungan Distribusi Pressure Drop Pada Sistem Perpipaan Satu Dimensi

B. Author Complete Name

Muhammad Resya Saputra

250656571

C. Affiliation

Departemen Teknik Mesin UI, Depok, Indonesia

D. Abstract

Summarize the report in 150–250 words, highlighting the objectives, methodology, key findings, and conclusions.

E. Author Declaration

Author akan berusaha mengikuti frame work DAI5 sebisa mungkin

5.1. Deep Awareness (of) I

Dengan tahap ini, author akan mendalami dan membangun kesadaran mengenai dampak dari proyek ini kepada diri author sendiri dan masyarakat

• Memberi manfaat bagi masyarakat dengan mengembangkan program penghitungan praktis
• Meningkatkan pemahaman mengenai dinamika fluida dalam pipa baik cara kerjanya maupun teori dibaliknya
• Membangun kesadaran terhadap pencipta dengan meniatkan pelaksanaan proyek sebagai suatu bentuk ibadah

5.2. Intention of the Project Activity

Dengan tahap ini, author akan mendalami tujuan dan motivasi author dalam pengerjaan proyek ini

• Membangun alat penghitung pressure drop pada sistem perpipaan yang dapat bermanfaat bagi masyarakat
• Mengembangkan alat penelitian dinamika fluida yang dapat berguna bagi masyarakat sebagai pembangkit listrik

F. Introduction

Dalam sistem konversi energi dan transportasi fluida, fenomena penurunan tekanan (pressure drop) merupakan parameter kritis dalam perancangan sistem perpipaan. Penurunan tekanan menentukan daya pompa yang dibutuhkan dan efisiensi keseluruhan sistem. Meskipun solusi analitik untuk aliran laminar dalam pipa lurus telah didefinisikan dengan baik (Hagen-Poiseuille), simulasi numerik menjadi pendekatan esensial untuk memahami dasar-dasar Computational Fluid Dynamics (CFD) sebelum melangkah ke geometri yang lebih kompleks.

6.1. Initial Thinking (about the Problem):

Pada tahap ini, author akan membongkar lebih lanjut mengenai dinamika fluida fenomena pressure drop pada pipa. Hasil dekomposisi yang ditemukan adalah:

• Secara fundamental, pressure drop adalah manifestasi dari konversi energi mekanik menjadi energi termal (panas) yang tidak dapat dipulihkan (irreversible) akibat resistansi aliran.
• Penyebab paling mendasar adalah Viskositas. Akibat gaya antar-molekul, lapisan yang bergerak lebih cepat akan “menarik” lapisan yang lebih lambat, dan lapisan yang lambat akan “menahan” lapisan yang cepat.
• Pada dinding pipa, kecepatan fluida adalah nol. Sementara di tengah pipa, kecepatan fluida maksimum. Perbedaan kecepatan yang drastis dari dinding ke tengah menciptakan Gradien Kecepatan. erdasarkan Hukum Viskositas Newton, gradien ini menghasilkan Tegangan Geser Dinding
• Diantara proses pengeluaran energi, energi keluaran yang dapat digunakan hanya berasal dari proses ekspansi sementara pada proses cooling energi hanya dibuang kelingkungan (terdapat kemungkinan penggunaan kembali menggunakan waste heat recovery)
• Pada fluida nyata (viscous), ada energi yang hilang. Tekanan tidak hilang begitu saja, melainkan terdisipasi menjadi panas akibat kerja gaya gesek viskos. Meskipun kenaikan suhunya mungkin sangat kecil (kecuali pada tekanan ekstrim), secara termodinamika energi kualitas tinggi (tekanan mekanis) telah terdegradasi menjadi energi kualitas rendah (internal heat).
• Jika aliran memiliki Bilangan Reynolds tinggi (Turbulen), mekanisme pressure drop bertambah parah karena Selain gesekan viskos, ada pertukaran momentum akibat pusaran (eddies). Partikel fluida bergerak acak, menabrak dinding dan satu sama lain secara kacau.Energi kinetik dari aliran rata-rata diambil untuk memutar pusaran-pusaran kecil ini, yang akhirnya musnah menjadi panas karena viskositas. Ini menyebabkan penurunan tekanan yang jauh lebih besar dibandingkan aliran laminar.

G. Methods & Procedures

Perhitungan distribusi pressure drop berfokus pada penyelesaian persamaan difusi tekanan satu dimensi (1D). Metode numerik yang digunakan adalah Metode Beda Hingga (Finite Difference Method – FDM) untuk mendiskritisasi persamaan diferensial parsial menjadi persamaan aljabar linear. Untuk menyelesaikan sistem persamaan linear tersebut, digunakan metode iteratif Gauss-Seidel yang dikenal efisien dalam penggunaan memori komputer dibandingkan metode eliminasi langsung, khususnya untuk matriks berukuran besar.

7.1. Idealization:

Pada tahap ini, author akan menjabarkan asumsi serta rumusan yang akan digunakan:

• Kondisi Tunak (Steady-State): Sifat-sifat aliran (tekanan dan kecepatan) pada setiap titik dianggap konstan terhadap waktu
• Fluida Inkompresibel (Incompressible Fluid): Densitas fluida ($\rho$) dianggap konstan sepanjang pipa, sehingga perubahan tekanan tidak mempengaruhi kerapatan fluida.sil proses heating)
• Aliran Satu Dimensi (1D): Analisis dibatasi pada variasi tekanan sepanjang sumbu aksial pipa
• Aliran Berkembang Penuh (Fully Developed Flow): Profil kecepatan dianggap telah terbentuk sempurna dan tidak berubah sepanjang pipa. Konsekuensinya, gradien tekanan akibat gesekan adalah konstan (linear).
• Efek Gravitasi Diabaikan: Pipa diasumsikan terpasang horizontal, sehingga perbedaan ketinggian bernilai nol dan tidak mempengaruhi perubahan tekanan.
• Berdasarkan asumsi di atas, persamaan konservasi momentum (Navier-Stokes) tereduksi menjadi persamaan diferensial biasa orde dua, yaitu Persamaan Laplace 1D. Persamaan ini menyatakan bahwa kelengkungan (curvature) dari profil tekanan adalah nol:

Untuk mendapatkan solusi unik dari persamaan diferensial di atas, diterapkan kondisi batas tipe Dirichlet pada kedua ujung domain komputasi:

Pada Inlet (x=0): P(0) = P in (Tekanan Masuk Diketahui)

Pada Outlet x = L: P(L) = P out (Tekanan Keluar Diketahui)

Penyelesaian analitik didekati menggunakan metode numerik dengan langkah-langkah berikut:

a. Diskritisasi FDM (Finite Difference Method) Turunan kedua didiskritisasi menggunakan skema Central Difference Approximation pada grid yang seragam

b. Skema Iterasi Gauss-Seidel Sistem persamaan linear diselesaikan secara iteratif. Berbeda dengan metode Jacobi, metode Gauss-Seidel menggunakan nilai terbaru k+1 dari node sebelumnya i-1 segera setelah dihitung, untuk mempercepat konvergensi

7.2. Instruction (Set):

Pada proses ini akan diberikan flowchart, penjelasan program serta kode python proyek ini.

Flowchartnya sebagai berikut:

Algoritma program bekerja dengan cara:

1. Program memulai dengan mendefinisikan konstanta fisik dan numerik: Panjang pipa, Tekanan Inlet, Tekanan Outlet, Jumlah Node, Maksimum Iterasi, dan Toleransi Error. Program menghitung jarak antar node
2. Dibuat array 1D sepanjang N untuk menyimpan nilai tekanan. Indeks pertama array i=0 diisi dengan nilai P in, dan indeks terakhir i=N-1 diisi dengan nilai P out. Seluruh node internal diinisialisasi dengan nilai awal sembarang untuk memulai perhitungan.
3. Program masuk ke dalam siklus perulangan (loop) utama yang akan berjalan dari iterasi k=1 hingga batas Max Iter. Sebelum melakukan pembaruan nilai, program menyalin array tekanan saat ini ke dalam variabel sementara sebagai acuan untuk menghitung error nanti.
4. Di dalam setiap iterasi, program melakukan looping spasial menelusuri setiap node internal dari i=1 hingga i=N-2. Pada setiap node, nilai tekanan diperbarui menggunakan rumus diskritisasi.
5. Setelah seluruh node diperbarui dalam satu siklus iterasi, program menghitung besar kesalahan (error) relatif antara solusi baru (P) dan solusi lama. Metode yang digunakan biasanya adalah L2 Norm (akar kuadrat dari jumlah kuadrat selisih) atau Max Absolute Difference.
6. Program membandingkan nilai error yang dihitung dengan Toleransi Error yang ditetapkan di awal. Jika Error < e, maka solusi dianggap telah konvergen (stabil). Program menghentikan iterasi (break loop) meskipun jatah iterasi maksimum belum habis. Jika iterasi mencapai batas maksimum (Max Iter) namun error masih tinggi, program berhenti dan memberikan peringatan bahwa solusi belum konvergen.
7. Hasil tekanan akhir pada setiap node disimpan ke dalam tabel data. Program membuat plot grafik hubungan antara Posisi Pipa (x) pada sumbu horizontal dan Tekanan P pada sumbu vertikal untuk memvisualisasikan profil gradien tekanan.

Kumpulan rumusnya adalah:

Metode Numerik dengan Finite Difference Method

H. Results & Discussion

Program tersebut telah berjalan dan hasilnya dapat ditonton pada:

Keluaran program berupa tabel distribusi tekanan dalam pipa beserta dengan grafik hasil perhitungan pressure drop dengan metode iterasi gauss seidel dan kurva error terhadap jumlah iterasi.

“

[INPUT PARAMETERS]

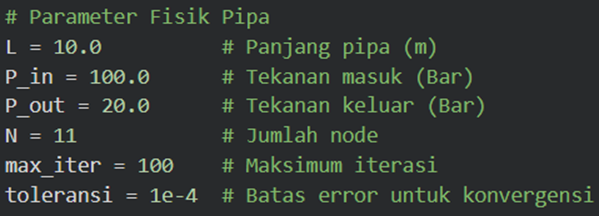
— RESULTS —

—————–

 Finish

“

Selain program, dibuat juga AI agent dengan mensupply knowledge. Berikut hasil testing AI agent

• Tester: Adamsyah Haryo

I. Conclusion, Closing Remarks, Recommendations

Proyek komputasi ini memberikan wawasan fundamental mengenai bagaimana hukum fisika yang kompleks dapat diselesaikan melalui pendekatan algoritmik. Meskipun model yang digunakan adalah penyederhanaan 1D, prinsip-prinsip diskritisasi, iterasi, dan analisis konvergensi yang diterapkan merupakan fondasi utama dalam simulasi Computational Fluid Dynamics (CFD) yang lebih lanjut.

Untuk pengembangan penelitian atau tugas selanjutnya agar lebih mendekati kondisi riil dan meningkatkan efisiensi komputasi, disarankan untuk memperluas domain simulasi menjadi 2 Dimensi (2D) untuk mengamati profil kecepatan parabolik (velocity profile) di sepanjang penampang pipa, tidak hanya penurunan tekanan.

J. Acknowledgments

Author mengucapkan terimakasih kepada Prof. Dr. Ahmad Indra serta teman teman di kelas komputasi teknik semester gasal 2025/2026 Teknik Mesin FTUI. Author juga berterimakasih terhadap AIDAI5 yang memungkinkan pembuatan AI agent.

K. (References) Literature Cited

Base Code Python pada proyek ini dibuat dengan bantuan Gemini AI.

L. Appendices

link drive dokumentasi

https://drive.google.com/drive/folders/1tvVMiDLDCok9N9FFRMistvRRc7ab37uP?usp=drive_link

Berikut kode python yang digunakan pada proyek ini

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Parameter Fisik Pipa
L = 10.0          # Panjang pipa (m)
P_in = 100.0      # Tekanan masuk (Bar)
P_out = 20.0      # Tekanan keluar (Bar)
N = 11            # Jumlah node
max_iter = 100    # Maksimum iterasi
toleransi = 1e-4  # Batas error untuk konvergensi

# Inisialisasi
dx = L / (N - 1)
x = np.linspace(0, L, N)

# Array tekanan dengan kondisi batas
P = np.zeros(N)
P[0] = P_in
P[-1] = P_out

# Simpan history iterasi
history = [P.copy()]
error_log = []

print("Memulai Iterasi Gauss-Seidel...")

# LOOP ITERASI GAUSS-SEIDEL
for k in range(1, max_iter + 1):
    P_old = P.copy()
    max_error = 0.0
    
    # UPDATE RULE GAUSS-SEIDEL [1]:
    # P_i = 0.5 * (P_{i-1} + P_{i+1})
    for i in range(1, N - 1):
        # Menggunakan P[i-1] yang baru diupdate dan P[i+1] yang masih lama
        P_new = 0.5 * (P[i-1] + P_old[i+1])
        
        current_error = abs(P_new - P_old[i])
        if current_error > max_error:
            max_error = current_error
        
        P[i] = P_new  # Immediate update - karakteristik Gauss-Seidel
    
    history.append(P.copy())
    error_log.append(max_error)
    
    # Cek Konvergensi
    if max_error < toleransi:
        print(f"Konvergensi tercapai pada iterasi ke-{k}")
        break
else:
    print("Maksimum iterasi tercapai")

# Solusi Analitik Linear [1]
P_analitik = P_in - ((P_in - P_out) / L) * x

# TABEL VALIDASI DATA
snapshots = {}
iter_to_show = [0, 1, 10, 50, -1]  # Iterasi yang akan ditampilkan

for idx in iter_to_show:
    if idx == -1:
        snapshots['Iterasi Akhir'] = history[-1]
    else:
        snapshots[f'Iterasi {idx}'] = history[min(idx, len(history)-1)]

df_data = {'Posisi Node (m)': x, 'Solusi Analitik': np.round(P_analitik, 4)}
for key, values in snapshots.items():
    df_data[key] = np.round(values, 4)

df = pd.DataFrame(df_data)
print("\n=== TABEL DISTRIBUSI TEKANAN ===")
print(df.to_string(index=False))

# VISUALISASI GRAFIK
plt.figure(figsize=(15, 5))

# Plot 1: Distribusi Tekanan
plt.subplot(1, 2, 1)
# Plot history iterasi (putus-putus)
iterations_to_plot = [0, 1, 2, 5, 10, -1]
colors = plt.cm.viridis(np.linspace(0, 1, len(iterations_to_plot)))

for j, iter_idx in enumerate(iterations_to_plot):
    if iter_idx == -1:
        label = 'Numerik Akhir'
        linestyle = '-'
        linewidth = 2
    else:
        label = f'Iter {iter_idx}'
        linestyle = '--'
        linewidth = 1
    
    if iter_idx < len(history):
        plt.plot(x, history[iter_idx], linestyle=linestyle, 
                color=colors[j], label=label, linewidth=linewidth)

plt.plot(x, P_analitik, 'r-', linewidth=2, label='Analitik (Eksak)')
plt.xlabel('Posisi Pipa (m)')
plt.ylabel('Tekanan (Bar)')
plt.title('Distribusi Pressure Drop - Gauss-Seidel')
plt.legend()
plt.grid(True)

# Plot 2: Kurva Konvergensi Error
plt.subplot(1, 2, 2)
plt.semilogy(range(1, len(error_log)+1), error_log, 'ro-', markersize=4)
plt.xlabel('Jumlah Iterasi')
plt.ylabel('Error Maksimum (Skala Log)')
plt.title('Kurva Konvergensi Gauss-Seidel')
plt.grid(True, which="both", ls="-")

plt.tight_layout()
plt.show()

# Komentar tentang Update Rule Gauss-Seidel
print("\n=== KOMENTAR UPDATE RULE GAUSS-SEIDEL ===")
print("""Update Rule: P[i] = 0.5 * (P[i-1] + P[i+1])

Karakteristik utama Gauss-Seidel [1]:
1. Immediate Update: Nilai yang baru dihitung langsung digunakan untuk node berikutnya
2. Faster Convergence: Dibandingkan Jacobi, konvergen lebih cepat karena menggunakan informasi terbaru
3. Sequential Processing: Perhitungan dilakukan secara berurutan dari kiri ke kanan
4. Memory Efficient: Hanya membutuhkan satu array tekanan (tidak perlu menyimpan iterasi sebelumnya)

Rumus ini berasal dari diskritisasi central difference persamaan Laplace: d²P/dx² = 0""")