Laporan Analisis Finite Element Analysis (FEA) dan Computational Fluid Dynamics (CFD) Terhadap Objek Wing Menggunakan Aplikasi SIEMENS STAR CCM+ | Aloysius Lesmono 2306206995 - Metode Numerik 01

Latar Belakang

Dalam era rekayasa modern yang semakin kompleks, pemodelan dan simulasi komputasi telah menjadi instrumen tak terpisahkan dalam siklus desain dan analisis. Pendekatan ini memungkinkan para insinyur untuk mengeksplorasi berbagai skenario, mengoptimalkan kinerja, dan mengidentifikasi potensi masalah tanpa perlu membangun prototipe fisik yang mahal dan memakan waktu. Di antara berbagai metode simulasi, Finite Element Analysis (FEA) dan Computational Fluid Dynamics (CFD) menonjol sebagai pilar utama. FEA, secara tradisional, banyak digunakan untuk menganalisis perilaku struktural material, perpindahan panas konduksi, dan fenomena medan lainnya pada benda padat. Namun, fleksibilitasnya telah meluas hingga diterapkan dalam disiplin ilmu lain. Di sisi lain, CFD secara spesifik fokus pada dinamika fluida, perpindahan panas konveksi, dan transportasi massa, memberikan kemampuan untuk memprediksi bagaimana fluida akan berperilaku dalam berbagai kondisi. Integrasi dan pemahaman mendalam tentang kedua metode ini sangat penting untuk mengatasi tantangan rekayasa kontemporer, dari desain aerodinamis kendaraan hingga optimasi sistem pendingin dan analisis lingkungan. Laporan ini akan menguraikan secara komprehensif bagaimana FEA diterapkan dalam konteks CFD, membahas metodologi simulasi, dan menyajikan analisis mendalam dari hasil simulasi CFD yang telah diberikan.

Pendahuluan

Computational Fluid Dynamics (CFD) adalah cabang ilmu yang mengaplikasikan metode numerik dan algoritma untuk menyelesaikan persamaan-persamaan yang mengatur aliran fluida. Ini adalah alat simulasi yang sangat kuat yang memungkinkan prediksi perilaku fluida dalam berbagai aplikasi, mulai dari rekayasa dirgantara hingga lingkungan industri. Inti dari banyak implementasi CFD modern adalah Finite Element Analysis (FEA), meskipun metode lain seperti Finite Volume Method (FVM) juga sangat populer. Dalam konteks CFD, FEA berfungsi sebagai metode numerik untuk memodelkan aliran fluida, perpindahan panas, atau fenomena transportasi lainnya dengan memecah domain fisika yang kompleks menjadi sejumlah elemen diskrit yang lebih kecil. Tujuan utama pendekatan ini adalah untuk mendapatkan solusi aproksimasi dari distribusi variabel-variabel kunci seperti kecepatan, tekanan, suhu, atau konsentrasi fluida di seluruh domain. Kemampuan FEA untuk menangani geometri yang sangat kompleks dan menyediakan solusi yang akurat menjadikannya pilihan yang berharga dalam analisis dan optimasi sistem rekayasa yang melibatkan interaksi fluida.

Tujuan

Tujuan dari laporan ini adalah untuk memberikan pemahaman yang komprehensif tentang aspek-aspek kunci dalam FEA dan CFD, serta menganalisis studi kasus yang diberikan:

Memahami Fondasi FEA dalam CFD: Menjelaskan secara rinci bagaimana prinsip-prinsip Finite Element Analysis (FEA) diadaptasi dan digunakan sebagai metode numerik untuk memecahkan masalah Computational Fluid Dynamics (CFD).
Menguraikan Metodologi Simulasi CFD: Memetakan langkah-langkah sistematis yang terlibat dalam melakukan simulasi CFD, mulai dari pre-processing (diskritisasi domain dan penentuan syarat batas) hingga post-processing (analisis dan visualisasi hasil).
Menganalisis Hasil Simulasi CFD secara Mendalam: Menginterpretasikan secara kritis visualisasi aliran (streamlines), peta kontur kecepatan, dan distribusi tekanan, serta data konvergensi numerik dari simulasi yang dilakukan dengan SIEMENS STAR-CCM+.
Mengidentifikasi Keunggulan dan Tantangan Aplikasi: Mengevaluasi kelebihan yang ditawarkan oleh FEA dalam penyelesaian masalah CFD, sekaligus mengidentifikasi tantangan dan keterbatasan yang perlu dipertimbangkan dalam implementasinya.
Menarik Kesimpulan dan Rekomendasi: Menyimpulkan temuan utama dari analisis dan memberikan rekomendasi untuk studi lebih lanjut atau aplikasi praktis.

Rumusan Masalah

Berdasarkan latar belakang dan tujuan yang telah ditetapkan, rumusan masalah yang akan dieksplorasi secara rinci dalam laporan ini adalah sebagai berikut:

Bagaimana prinsip diskritisasi domain dan pemodelan elemen dalam FEA berkontribusi pada representasi akurat dari sistem aliran fluida yang kompleks dalam CFD?
Apa peran dan signifikansi persamaan Navier-Stokes (Kontinuitas, Momentum, Energi) sebagai fondasi matematis dalam simulasi CFD, dan bagaimana FEA mengaproksimasi solusinya?
Bagaimana interpretasi visualisasi aliran (streamlines), kontur kecepatan, dan peta tekanan dapat memberikan wawasan yang mendalam tentang karakteristik aerodinamis atau hidrodinamis suatu objek dalam simulasi CFD?
Bagaimana data konvergensi numerik, khususnya residual untuk persamaan konservasi dan stabilitas parameter integral seperti koefisien drag dan gaya drag, digunakan untuk memvalidasi keandalan dan akurasi solusi simulasi CFD?
Apa implikasi praktis dari keunggulan FEA dalam menangani geometri kompleks dan fleksibilitasnya untuk berbagai masalah, serta bagaimana tantangan komputasi intensif dan sensitivitas terhadap kualitas mesh diatasi dalam praktik simulasi CFD?

Dasar Teori

1. Finite Element Analysis (FEA) dalam CFD: Pendekatan Numerik yang Kuat

Finite Element Analysis (FEA) adalah metode numerik yang serbaguna, digunakan dalam CFD untuk memodelkan perilaku aliran fluida, perpindahan panas, dan fenomena transportasi massa dengan memecah domain studi yang kompleks menjadi sejumlah elemen yang lebih kecil dan terdefinisi dengan baik. Elemen-elemen ini, yang bisa berupa segitiga, segiempat, tetrahedron, atau hexahedron, saling terhubung pada titik-titik yang disebut node. Tujuan utama FEA dalam konteks CFD adalah untuk mendapatkan solusi aproksimasi yang akurat dari variabel-variabel medan seperti kecepatan, tekanan, dan suhu di seluruh domain fluida.

Proses FEA dalam CFD melibatkan serangkaian langkah sistematis:

Diskritisasi Domain (Meshing): Langkah awal adalah membagi domain fluida kontinu menjadi mesh diskrit yang terdiri dari elemen-elemen kecil. Kualitas mesh—ukuran, bentuk, dan kerapatannya—sangat krusial. Mesh yang lebih halus (elemen yang lebih kecil) umumnya menghasilkan akurasi yang lebih tinggi tetapi dengan biaya komputasi yang jauh lebih besar. Penting untuk mengoptimalkan mesh di daerah dengan gradien variabel yang tinggi (misalnya, lapisan batas, daerah wake) untuk menangkap detail aliran secara akurat.
Pemodelan Elemen (Formulasi Persamaan Lokal): Untuk setiap elemen diskrit, persamaan matematis diturunkan berdasarkan hukum-hukum fisika yang berlaku, seperti persamaan Navier-Stokes untuk momentum dan persamaan energi untuk perpindahan panas. Dalam FEA, variabel-variabel seperti kecepatan dan tekanan dalam elemen diaproksimasi menggunakan fungsi interpolasi (sering disebut fungsi bentuk atau shape function) yang menghubungkan nilai-nilai pada node elemen ke nilai di dalam elemen. Ini mengubah masalah diferensial kontinu menjadi sistem aljabar linear atau non-linear untuk setiap elemen.
Pemasangan Sistem Global (Assembly): Setelah persamaan untuk setiap elemen diformulasikan, persamaan-persamaan ini kemudian digabungkan atau “dipasang” menjadi sistem persamaan aljabar global yang mewakili seluruh domain fluida. Proses ini memastikan konservasi besaran fisik di seluruh domain dan di antara elemen-elemen yang berdekatan.
Penerapan Syarat Batas (Boundary Conditions): Kondisi fisik pada batas-batas domain fluida harus ditentukan secara eksplisit. Syarat batas ini sangat penting karena mempengaruhi solusi secara keseluruhan dan harus mencerminkan kondisi fisik sebenarnya. Contoh syarat batas meliputi:
- Inlet Velocity/Pressure: Kecepatan atau tekanan fluida yang masuk ke domain.
- Outlet Pressure/Flow: Tekanan atau karakteristik aliran di titik keluar domain.
- No-Slip Wall: Asumsi bahwa fluida menempel pada permukaan padat, sehingga kecepatan fluida relatif terhadap dinding adalah nol (umum untuk aliran viskos).
- Symmetry: Digunakan untuk mengurangi ukuran domain komputasi jika ada simetri geometris dan aliran.
- Periodicity: Untuk aliran yang berulang secara periodik.
Penyelesaian Numerik (Solving): Sistem persamaan aljabar global yang dihasilkan, yang seringkali sangat besar dan non-linear, diselesaikan menggunakan algoritma numerik iteratif pada komputer. Algoritma ini dirancang untuk menemukan nilai-nilai variabel di setiap node yang memenuhi semua persamaan dan syarat batas. Karena sifat non-linearitas persamaan Navier-Stokes, proses penyelesaian biasanya bersifat iteratif, di mana solusi diupdate secara bertahap hingga konvergensi tercapai.
Analisis Hasil (Post-Processing): Setelah solusi diperoleh, hasil disajikan dalam bentuk yang mudah diinterpretasikan. Ini termasuk visualisasi aliran (misalnya, streamlines, vektor kecepatan), peta kontur distribusi kecepatan, tekanan, suhu, atau turbulensi, serta plot numerik dari parameter-parameter kunci seperti gaya hambat atau gaya angkat. Tahap ini juga melibatkan validasi hasil terhadap data eksperimen atau solusi analitis jika tersedia.

2. Persamaan Dasar Computational Fluid Dynamics (CFD)

Inti matematis dari CFD terletak pada persamaan Navier-Stokes, yang merupakan pernyataan hukum konservasi massa, momentum, dan energi untuk fluida. Untuk aliran kompresibel dan transien, bentuk umum persamaan ini cukup kompleks, tetapi untuk banyak aplikasi, bentuk yang disederhanakan (misalnya, aliran inkompresibel, tunak) dapat digunakan.

Persamaan Kontinuitas (Konservasi Massa):
Persamaan ini menyatakan bahwa massa fluida tidak dapat diciptakan atau dimusnahkan. Untuk aliran inkompresibel, ini sering disederhanakan menjadi:

Di mana u adalah vektor kecepatan fluida. Ini berarti bahwa tidak ada akumulasi atau kehilangan massa dalam volume kontrol.
Persamaan Momentum (Konservasi Momentum):
Berdasarkan hukum kedua Newton, persamaan ini menggambarkan bagaimana perubahan momentum fluida dipengaruhi oleh gaya-gaya yang bekerja padanya (gaya tekanan, gaya viskos, dan gaya tubuh seperti gravitasi). Ada tiga persamaan momentum, satu untuk setiap arah spasial (x, y, z). Dalam bentuk tensor umum untuk aliran inkompresibel:

Di mana:
- ρ adalah densitas fluida.
- t adalah waktu.
- p adalah tekanan.
- μ adalah viskositas dinamis fluida.
- f adalah gaya tubuh per unit volume.
- ∂t∂u adalah suku transien (perubahan waktu).
- (u⋅∇)u adalah suku konvektif (transportasi momentum oleh aliran itu sendiri).
- −∇p adalah suku gradien tekanan.
- μ∇2u adalah suku viskos (difusi momentum).
Persamaan Energi (Konservasi Energi): 23
Persamaan ini diterapkan jika ada transfer panas dalam sistem. Ini menggambarkan bagaimana energi total fluida (termasuk energi internal, kinetik, dan potensial) berubah karena kerja yang dilakukan oleh tekanan dan gaya viskos, serta transfer panas melalui konduksi dan konveksi.

Di mana:
- T adalah suhu.
- Cp adalah kapasitas panas spesifik pada tekanan konstan.
- k adalah konduktivitas termal.
- Φ adalah fungsi disipasi viskos (konversi energi kinetik menjadi energi internal karena viskositas).
- Q adalah sumber panas.

Dalam FEA, persamaan diferensial parsial ini diubah menjadi sistem persamaan aljabar diskrit yang dapat diselesaikan secara numerik. Fungsi interpolasi (fungsi bentuk) digunakan untuk merepresentasikan variabel-variabel fluida di dalam setiap elemen berdasarkan nilai-nilai nodal.

3. Keunggulan dan Tantangan FEA dalam CFD

Penerapan FEA untuk masalah CFD menawarkan berbagai keunggulan, tetapi juga dihadapkan pada beberapa tantangan:

Keunggulan:

Penanganan Geometri Kompleks: Salah satu kekuatan terbesar FEA adalah kemampuannya untuk menangani domain dengan geometri yang sangat kompleks dan tidak beraturan. Ini karena mesh elemen dapat disesuaikan secara fleksibel dengan bentuk objek, memungkinkan representasi yang akurat dari fitur-fitur rumit seperti bilah turbin, manifold, atau sayap pesawat.
Akurasi Tinggi untuk Berbagai Rejim Aliran: FEA dapat memberikan hasil yang sangat akurat untuk berbagai rejim aliran, termasuk aliran laminar dan turbulen, asalkan resolusi mesh yang memadai digunakan. Kemampuan untuk memfokuskan mesh (refinement) di daerah-daerah kritis (misalnya, lapisan batas, daerah shear tinggi) memungkinkan penangkapan fenomena fisik secara detail.
Fleksibilitas Multi-fisika: FEA sangat fleksibel dan dapat diperluas untuk mencakup masalah multi-fisika, di mana interaksi antara berbagai fenomena fisik (misalnya, aliran fluida, perpindahan panas, deformasi struktural, reaksi kimia) dipertimbangkan secara simultan. Ini memungkinkan simulasi sistem yang lebih realistis dan terintegrasi.
Variasi Elemen dan Fungsi Orde Tinggi: FEA memungkinkan penggunaan berbagai jenis elemen (misalnya, linear, kuadratik) dan fungsi interpolasi orde tinggi, yang dapat meningkatkan akurasi solusi dengan jumlah elemen yang lebih sedikit dibandingkan metode orde rendah.
Basis Teori yang Kuat: FEA memiliki basis teori matematika yang kuat, yang mendukung konvergensi dan stabilitas solusi jika diimplementasikan dengan benar.

Tantangan:

Komputasi Intensif: Simulasi CFD, terutama untuk aliran turbulen atau domain besar dengan mesh halus, membutuhkan sumber daya komputasi yang sangat besar. Persamaan Navier-Stokes yang non-linear dan jumlah elemen yang besar menghasilkan sistem persamaan yang masif yang memerlukan waktu komputasi yang lama dan memori yang besar.
Kebutuhan Syarat Batas yang Tepat: Hasil simulasi sangat bergantung pada penetapan syarat batas yang akurat dan representatif dari kondisi fisik sebenarnya. Kesalahan dalam menentukan inlet velocity, outlet pressure, atau kondisi dinding dapat menyebabkan hasil yang tidak akurat atau bahkan ketidakstabilan numerik. Memperoleh data syarat batas yang akurat seringkali memerlukan pengukuran eksperimental.
Sensitivitas terhadap Kualitas Mesh: Kualitas mesh (ukuran, bentuk, dan ortogonalitas elemen) secara langsung memengaruhi akurasi dan stabilitas solusi. Mesh yang buruk dapat menyebabkan solusi yang divergen, hasil yang salah, atau konvergensi yang lambat. Proses pembuatan mesh yang berkualitas tinggi, terutama untuk geometri kompleks, bisa menjadi tantangan tersendiri dan memakan waktu.
Penanganan Turbulensi: Pemodelan turbulensi masih menjadi salah satu tantangan terbesar dalam CFD. Meskipun ada berbagai model turbulensi (seperti RANS, LES, DNS), masing-masing memiliki keterbatasan dan biaya komputasi yang bervariasi. Memilih model turbulensi yang tepat dan memvalidasinya untuk aplikasi spesifik memerlukan keahlian dan pengalaman.
Konvergensi dan Stabilitas Numerik: Memastikan konvergensi solusi dan stabilitas numerik bisa menjadi sulit, terutama untuk masalah aliran yang kompleks dengan non-linearitas tinggi. Pemilihan skema diskritisasi, strategi iterasi, dan parameter solver yang tepat sangat krusial.

Pengolahan Data

Data yang digunakan untuk analisis berasal dari hasil simulasi yang dijalankan menggunakan perangkat lunak SIEMENS STAR-CCM+, sebuah aplikasi terkemuka dalam bidang CFD. Data ini mencakup dua kategori utama:

Data Visualisasi Hasil Simulasi: Tiga gambar visualisasi disediakan, yang menampilkan representasi grafis dari karakteristik aliran fluida di sekitar objek 3D yang disimulasikan.
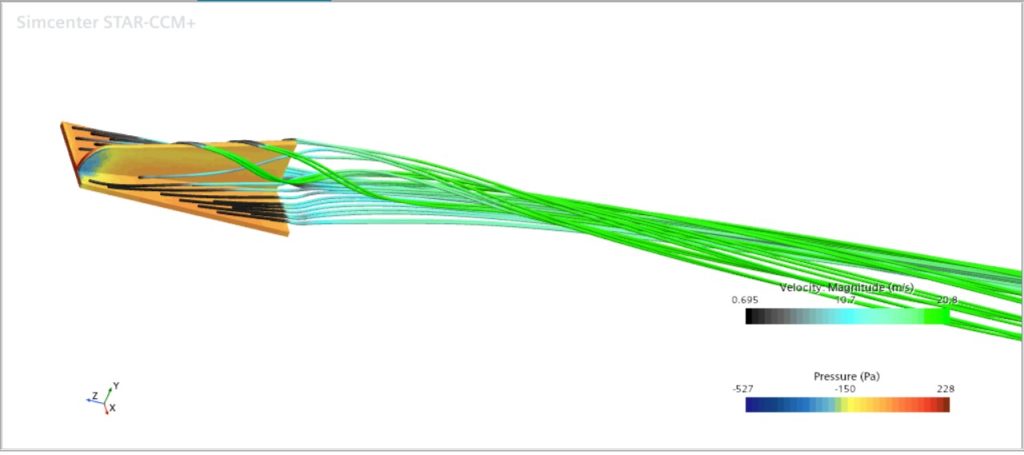
- Gambar 1 : Menampilkan pandangan samping dari objek dengan streamlines berwarna hijau dan biru muda. Sebuah skala warna untuk Velocity Magnitude (0.695 m/s hingga 20.8 m/s) dan Pressure (-527 Pa hingga 228 Pa) disajikan di sisi kanan.
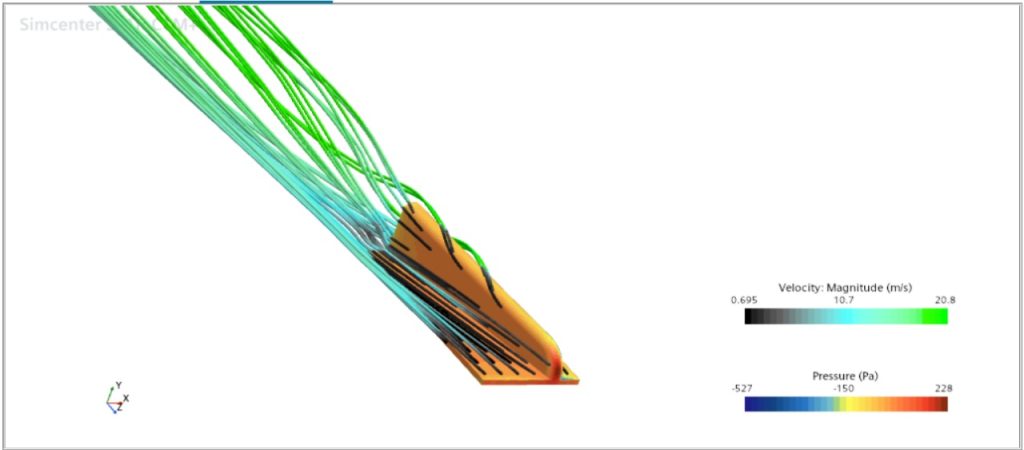
- Gambar 2 : Menampilkan pandangan serupa dari sudut yang sedikit berbeda, memberikan perspektif tambahan tentang pola aliran. Skala warna kecepatan dan tekanan identik dengan gambar sebelumnya.
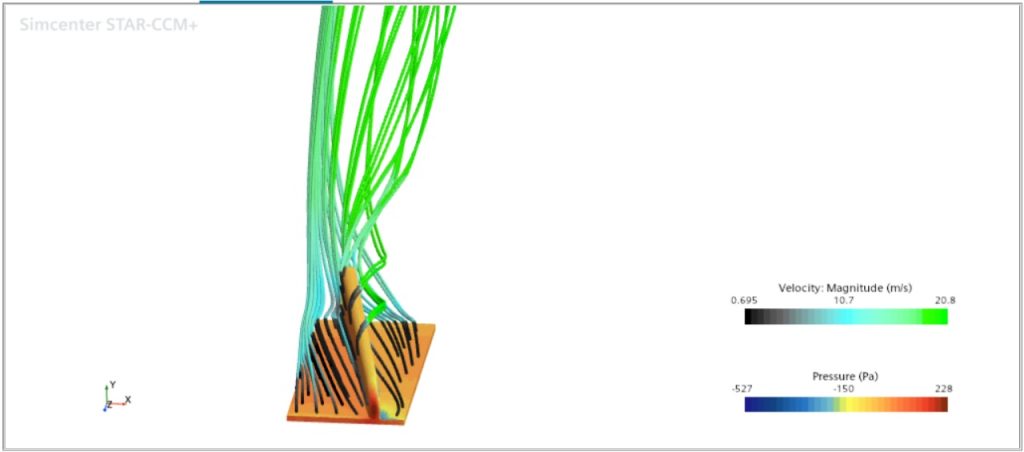
- Gambar 3: Menampilkan pandangan dari atas objek, menunjukkan bagaimana aliran berinteraksi dengan permukaan atas dan samping objek. Skala warna kecepatan dan tekanan juga konsisten. Data visual ini diinterpretasikan untuk memahami pola aliran kualitatif dan distribusi kuantitatif dari kecepatan dan tekanan.
Data Konvergensi Numerik: Satu gambar berupa tabel numerik (Tabel Hasil) menyajikan nilai-nilai residual dan parameter integral selama beberapa iterasi terakhir dari simulasi. Kolom-kolom dalam tabel mencakup:
- Iteration: Nomor iterasi simulasi (dari 941 hingga 946).
- Continuity: Residual persamaan kontinuitas.
- X-momentum, Y-momentum, Z-momentum: Residual persamaan momentum di masing-masing arah koordinat.
- Tke (Turbulent Kinetic Energy): Residual untuk persamaan transport Tke (jika model turbulensi K-Epsilon atau K-Omega digunakan).
- Tdr (Turbulent Dissipation Rate): Residual untuk persamaan transport Tdr (jika model turbulensi K-Epsilon atau K-Omega digunakan).
- Coefficient Drag: Nilai koefisien hambatan aerodinamis.
- Drag Force (N): Nilai gaya hambat dalam Newton. Data ini dianalisis untuk mengevaluasi apakah simulasi telah mencapai konvergensi yang memadai dan untuk mengkonfirmasi stabilitas solusi.

Analisis

1. Analisis Visualisasi Aliran (Streamlines, Kecepatan, dan Tekanan)

Visualisasi dari simulasi SIEMENS STAR-CCM+ memberikan gambaran yang kaya dan detail mengenai interaksi antara fluida dan objek. Objektif utama dari analisis visual ini adalah untuk memahami perilaku aliran secara kualitatif dan mengidentifikasi area-area kritis yang menunjukkan karakteristik aliran tertentu.

Pola Aliran (Streamlines):
- Garis-garis hijau terang yang dominan pada gambar merepresentasikan streamlines, yang menunjukkan jalur yang akan dilalui oleh partikel fluida jika aliran berada dalam kondisi tunak (steady state). Dari pandangan yang disediakan, terlihat jelas bahwa aliran fluida datang dari sisi kiri dan mengelilingi objek berbentuk aerodinamis (kemungkinan seperti sayap, fin, atau bagian dari badan kendaraan).
- Di bagian depan objek (sisi yang berhadapan langsung dengan aliran), streamlines cenderung menyebar dan melambat, mengindikasikan pembentukan titik stagnasi.
- Pada permukaan atas dan bawah objek, streamlines terlihat rapat dan mengikuti kontur objek. Kerapatan streamlines ini menunjukkan percepatan aliran di area tersebut.
- Di bagian belakang objek, streamlines terlihat lebih tidak teratur, menunjukkan pembentukan wake (daerah pusaran atau resirkulasi). Adanya streamlines berwarna biru muda di area ini kemungkinan besar mengindikasikan kecepatan aliran yang lebih rendah atau daerah dengan intensitas turbulensi yang lebih tinggi. Pembentukan wake ini sangat relevan karena berkontribusi signifikan terhadap gaya hambat (drag force) pada objek.
- Secara keseluruhan, pola streamlines menunjukkan adanya aliran yang lancar di sekitar sebagian besar permukaan objek, dengan kemungkinan adanya pemisahan aliran (flow separation) di daerah tertentu, terutama di bagian belakang atau di sudut-sudut tajam objek.
Distribusi Kecepatan (Velocity Magnitude):
- Skala warna untuk kecepatan berkisar dari 0.695 m/s (biru gelap) hingga 20.8 m/s (merah).
- Area dengan warna biru gelap atau hijau muda menunjukkan daerah dengan kecepatan fluida rendah. Ini sangat terlihat di bagian depan objek (titik stagnasi) di mana fluida melambat drastis saat berinteraksi dengan permukaan. Area kecepatan rendah juga mungkin terjadi di daerah wake di belakang objek, di mana terjadi resirkulasi dan energi kinetik fluida telah hilang akibat turbulensi dan gesekan.
- Area dengan warna kuning atau merah menunjukkan daerah dengan kecepatan fluida tinggi. Ini terjadi di mana streamlines sangat rapat dan fluida terpaksa mempercepat alirannya melalui ruang yang lebih sempit (efek Bernoulli). Untuk objek aerodinamis, ini sering terjadi di atas atau di bawah permukaan, tergantung pada desainnya, di mana tekanan menurun sebagai konsekuensi dari peningkatan kecepatan.
- Gradien warna yang jelas menunjukkan variasi kecepatan yang dinamis di sekitar objek, mencerminkan bagaimana energi kinetik fluida diubah saat melewati dan berinteraksi dengan objek.
Distribusi Tekanan (Pressure):
- Skala warna untuk tekanan berkisar dari -527 Pa (biru gelap) hingga 228 Pa (merah).
- Area dengan warna merah (tekanan tinggi) terlihat di bagian depan objek yang secara langsung menghadapi aliran. Ini adalah daerah di mana energi kinetik fluida diubah menjadi energi tekanan saat fluida melambat. Tekanan tinggi di bagian depan ini adalah kontributor utama terhadap gaya hambat bentuk (form drag).
- Area dengan warna biru gelap (tekanan rendah atau negatif) biasanya terjadi di atas atau di bawah objek di mana aliran dipercepat (berdasarkan prinsip Bernoulli), atau di daerah wake di belakang objek. Tekanan rendah di daerah wake menciptakan gaya hisap yang menarik objek ke belakang, menambah gaya hambat. Jika objek dirancang untuk menghasilkan gaya angkat (lift), tekanan rendah juga akan terbentuk di sisi atas (untuk profil sayap) atau sisi bawah (untuk profil terbalik).
- Perbedaan tekanan yang signifikan antara bagian depan dan belakang objek, serta antara sisi atas dan bawah, adalah faktor kunci dalam pembentukan gaya aerodinamis seperti gaya hambat dan gaya angkat.

Singkatnya, visualisasi ini secara efektif mengkomunikasikan kompleksitas aliran fluida di sekitar objek 3D. Ini menyoroti daerah-daerah penting dari interaksi fluida-objek, termasuk lokasi stagnasi, percepatan aliran, pembentukan wake, dan distribusi tekanan yang menghasilkan gaya aerodinamis.

2. Analisis Data Konvergensi Numerik

Konvergensi adalah aspek paling krusial dalam simulasi CFD. Ini menunjukkan bahwa solusi numerik telah mencapai kondisi stabil di mana perubahan nilai-nilai variabel dari satu iterasi ke iterasi berikutnya berada di bawah ambang batas yang dapat diterima. Data konvergensi yang disediakan menunjukkan perilaku residu dan parameter integral selama iterasi terakhir simulasi.

Residual Persamaan Konservasi (Kontinuitas, Momentum, Tke, Tdr):
- Residual adalah nilai error yang mengindikasikan seberapa baik persamaan konservasi (massa, momentum, energi) terpenuhi di setiap titik dalam domain. Semakin kecil nilai residual, semakin baik konvergensi solusi.
- Dalam data yang diberikan (Iterasi 941 hingga 946), nilai residual untuk Kontinuitas, X-momentum, Y-momentum, Z-momentum, Tke (Turbulent Kinetic Energy), dan Tdr (Turbulent Dissipation Rate) berada pada orde 10−6 hingga 10−9. Secara spesifik:
  - Kontinuitas: 1.4×10−6 hingga 1.4×10−6
  - Momentum (X, Y, Z): 7×10−7 hingga 3×10−8
  - Tke: 2×10−9 hingga 2×10−9
  - Tdr: 1×10−7 hingga 1×10−7
- Nilai-nilai ini sangat rendah dan menunjukkan bahwa persamaan-persamaan governing telah diselesaikan hingga tingkat akurasi yang sangat tinggi. Dalam praktik rekayasa, residual di bawah 10−4 atau 10−5 sering dianggap cukup untuk sebagian besar aplikasi. Nilai yang lebih rendah dari itu menunjukkan tingkat keyakinan yang tinggi terhadap stabilitas dan akurasi solusi yang diperoleh.
- Konsistensi nilai-nilai residual yang rendah ini menunjukkan bahwa simulasi telah berjalan untuk sejumlah besar iterasi sebelumnya dan telah memasuki fase konvergensi yang stabil, di mana solusi tidak lagi mengalami fluktuasi yang signifikan.
Parameter Integral (Coefficient Drag dan Drag Force):
- Coefficient Drag (Koefisien Hambat): Nilai Coefficient Drag terlihat sangat stabil pada 2.515317×10−4 di seluruh iterasi yang ditampilkan. Koefisien drag adalah parameter non-dimensi yang sangat penting dalam aerodinamika, yang mengukur efisiensi aerodinamis objek dalam hal resistansi terhadap gerakan melalui fluida. Stabilitas nilai ini adalah indikator utama bahwa gaya-gaya integral pada objek telah mencapai nilai steady-state.
- Drag Force (Gaya Hambat): Nilai Drag Force juga menunjukkan stabilitas yang sangat baik, berada di sekitar 5.030634×10−2 Newton. Gaya hambat adalah gaya resistif yang bekerja berlawanan arah dengan gerakan objek. Stabilitas nilai gaya hambat merupakan indikator kuat bahwa simulasi telah konvergen secara fisik, dan gaya total yang bekerja pada objek telah mencapai keseimbangan.

Interpretasi Keseluruhan Konvergensi:

Konvergensi yang sangat baik yang ditunjukkan oleh nilai residual yang rendah dan stabilitas parameter integral menegaskan bahwa hasil simulasi (yaitu, visualisasi kecepatan dan tekanan) adalah representasi yang andal dan akurat dari kondisi aliran tunak di sekitar objek. Ini berarti bahwa kita dapat memiliki kepercayaan tinggi pada prediksi performa aerodinamis objek berdasarkan simulasi ini. Jika simulasi tidak konvergen, hasil visualisasi akan menunjukkan pola yang tidak stabil atau tidak masuk akal, dan parameter integral akan terus berfluktuasi. Oleh karena itu, data konvergensi ini adalah bukti validitas dan keandalan simulasi yang telah dilakukan.

Kesimpulan

Laporan ini telah membahas secara komprehensif Finite Element Analysis (FEA) dalam konteks Computational Fluid Dynamics (CFD), metodologi simulasi, dan analisis mendalam dari hasil yang diberikan. Beberapa poin kunci dapat disimpulkan:

FEA sebagai Metode Dasar CFD: FEA adalah metode numerik yang kuat dan fleksibel yang memungkinkan simulasi aliran fluida, perpindahan panas, dan fenomena transportasi massa dengan memecah domain menjadi elemen-elemen diskrit. Ini adalah pendekatan yang efektif untuk mengaproksimasi solusi persamaan Navier-Stokes yang kompleks.
Metodologi Simulasi yang Terstruktur: Proses simulasi CFD melibatkan serangkaian langkah krusial, mulai dari diskritisasi domain yang cermat, formulasi persamaan elemen, pemasangan sistem global, penerapan syarat batas yang tepat, penyelesaian numerik yang iteratif, hingga analisis dan visualisasi hasil. Setiap langkah ini harus dilakukan dengan hati-hati untuk memastikan akurasi dan stabilitas solusi.
Wawasan dari Visualisasi Aliran: Visualisasi streamlines, peta kontur kecepatan, dan distribusi tekanan dari simulasi SIEMENS STAR-CCM+ memberikan wawasan yang sangat berharga tentang interaksi fluida-objek. Dari visualisasi ini, kita dapat mengidentifikasi daerah stagnasi, percepatan aliran, pembentukan wake, dan variasi tekanan yang berkontribusi pada gaya aerodinamis pada objek.
Konvergensi Solusi yang Andal: Data konvergensi menunjukkan bahwa simulasi telah mencapai konvergensi yang sangat baik, ditunjukkan oleh nilai residual yang sangat rendah untuk persamaan konservasi (orde 10−6 hingga 10−9) dan stabilitas sempurna pada nilai koefisien drag (2.515317×10−4) dan gaya drag (5.030634×10−2 N). Ini menegaskan keandalan dan akurasi hasil simulasi.
Keunggulan dan Tantangan Aplikasi Nyata: Meskipun FEA dalam CFD unggul dalam menangani geometri kompleks, fleksibilitas multi-fisika, dan potensi akurasi tinggi , tantangan signifikan tetap ada, termasuk kebutuhan komputasi intensif, sensitivitas terhadap kualitas mesh, dan penentuan syarat batas yang akurat.