ccitonline.com

Zahran Nadhif Afdallah Malik-2306155451

Metode Bisection adalah salah satu metode yang digunakan untuk menemukan akar persamaan dari sebuah fungsi dalam kurun interval[a,b]. ada beberapa syarat agar metode bisection dapat digunakan untuk menemukan akar persamaan, yaitu:

1. dalam interval [a,b], fungsi f(x) bersifat kontinu
2. dalam interval[a,b], terdapat sebuah akar persamaan, dengan demikian, nilai f(x) pada ujung interval f(a) dan f(b) akan berlawanan tanda

Nilai tengah yang membagi interval [a,b] adalah estimasi pertama akar dari persamaan numerik(Xns). akar aktual akan berada di salah satu interval [a,xNS] atau [xNS,b]. Iterasi kemudian dilakukan untuk mempersempit lebar interval yang memuat akar persamaan dengan menentukan nilai tengah interval berikutnya, sampai diperoleh nilai tengah yang mendekati nilai solusi numerik dengan tingkat ketelitian (batas toleransi) yang ditetapkan.

Berikut merupakan ilustrasi metode bisection

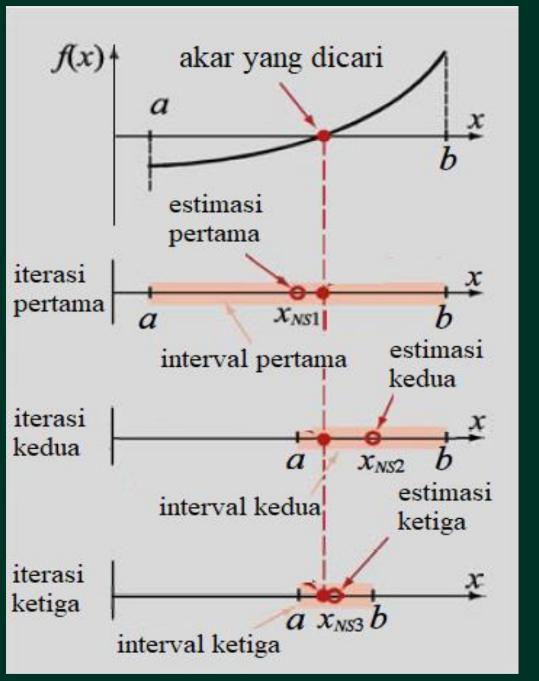
Algoritma dalam Metode Bisection:

1. tentukan fungsi f(x)
2. tentukan nilai interval a dan ba([a,b])
3. tentukan toleransi e dan batas iterasi maksimum N
4. periksa kondisi berikut
   • jika f(a) x f(b) >0, maka tidak ada akar diantara x=a dan x=b dan proses dihentikan.
   • jika f(a) x f(b) <0, maka terdapat akar diantara x=a dan x=b dan proses iterasi dimulai
5. hitung nilai tengah xNS= (a+B)/2, dan hitung f(xNS)
6. Periksa, jika f(xNS). f(a) < 0 maka b = xNS dan f(b) = f(xNS). Bila tidak a = xNS dan f(a) = f(xNS)
7. Ulangi langkah (5) sampai kriteria konvergensi tercapai dan didapatkan akar persamaan x = xNS
8. konvergensi tercapai bila salah satu kriteria tercapai
   • toleransi terpenuhi :

• jumlah iterasi melampaui batas iterasi N

Kelebihan dan Kekurangan Metode Bisection

1. Kelebihan
   • sederhana dan mudah diimplementasikan
   • evaluasi hanya satu nilai fungsi setiap iterasinya
   • tidak membutuhkan derivatif fungsi
2. kekurangan
   • konvergensi lambat

contoh koding metode bisection untuk phyton

berikut adalah contoh koding pada phyton untuk menemukan akar fungsi f(x) = X^3-5X+2

Link simulasi cfdsof pada heat conduction 2d